| HEAT
TRANSFER |
| With the cooperation and under supervision of our past president Ir. H.
Ghys |
| In practice heat transfer is the sum of the heat
transfer that takes place through conductivity, convection and radiation.
The relation below applies: |
| q = k x A x∆T x t |
q : The quantity of heat ( j )
k : total heat transfer
coeff. ( W/m2 x K) |
A : area (m2)
∆T = temperature difference |
t : time ( s ) |
Heat transfer frequently occurs between two bodies,
separated by a wall.
For such a (clean) flat wall the relation below applies: |
| 1/k = 1/α1 + d/λ + 1/α2 |
k : total heat transfer coeff. ( W/m2
x K)
α = heat transfer coefficient on respective
sides of the wall ( W/m2 x K ) |
d = thickness of the wall ( m ) |
λ = coefficient of thermal conductivity
for the wall (W/m x K) |
| The transferred quantity of heat in a heat
exchanger, is at each point a function of the prevailing heat difference
and the total heat transfer coefficient. Applicable to the entire heat
transfer surface is: |
| Q = k x A x LMTD |
Q = tranferred quantity oh heat ( Watt )
k = total heat
transfer coeff. (W/m2 x K) |
A = heat transferring surface (m2) |
LMTD = logarithmic mean temperature
diff. ( K ) |
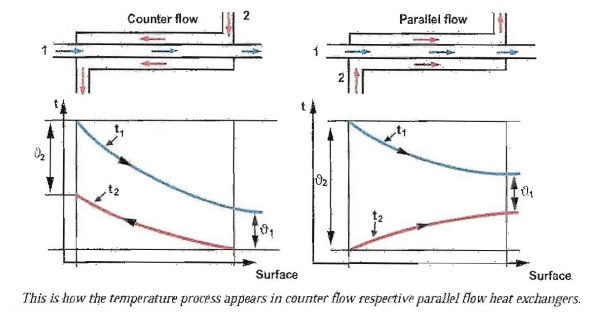
| The logarithmic mean temperature difference is defined as the
relation between the temperature difference at the heat exchanger's
two connection sides according to the expression: |
|
LMTD = (Δ1- Δ2 / ( In Δ1 / Δ2 ) |
| LMTD
= logarithmic mean tempt. diff.(K) |
Δ1 = the tempt. difference ( K ) |
Δ2 = the temperature difference ( °K ) |
 |
